Non-linear Reconstruction

The late-time matter distribution is highly non-Gaussian due to the non-linear gravitational evolution, making the 2-pt function inefficient when extracting information from small-scale structures. Iterative reconstruction can recover the initial Gaussian density field with high fidelity, thus allowing us to extract more information from the density field using only the 2-pt function. Based on the dark matter particle catalogs of the Quijote simulation, we compare the Fisher information contained in the reconstructed power spectrum and the non-linear power spectrum. We find that the iterative reconstruction can potentially improve the measurement of $\Omega_m, \Omega_b, h, n_s, \sigma_8$ and $M_\nu$ by a factor of 2.9, 2.4, 2.4, 2.5, 2.8 and 2.9 respectively. We also compare the information content of the reconstructed power of the iterative and linear reconstruction. These two reconstruction algorithms give similar results on large scales, while the iterative reconstruction performs better on small scales than the linear reconstruction.

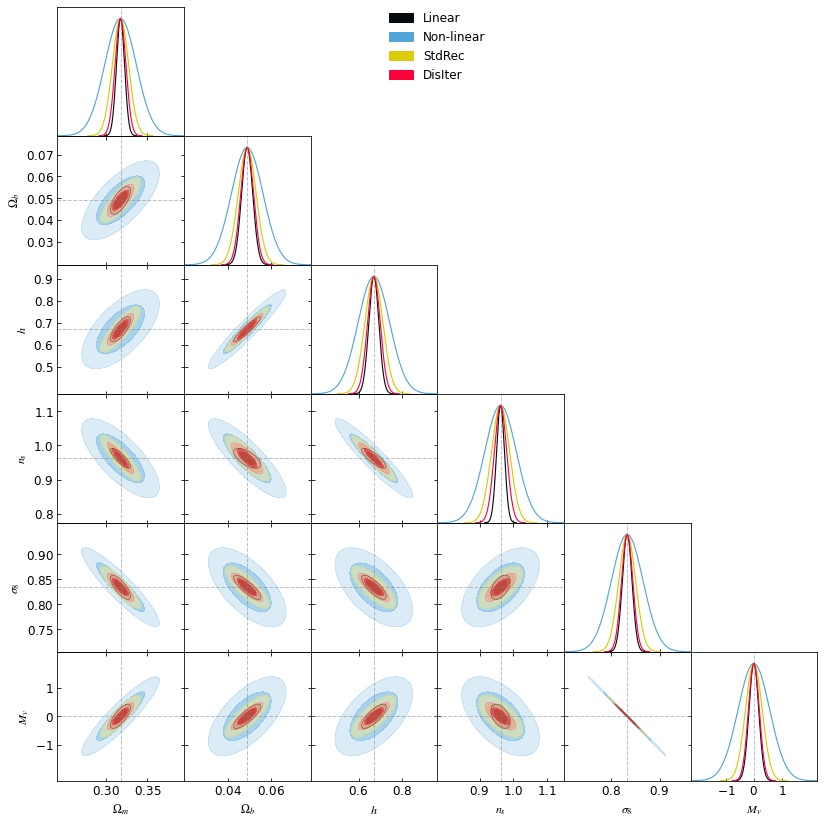
This figure shows the Fisher error of the post-reconstruction power at cutoff scale $k_{\mathrm{max}} = 0.5 \ h\mathrm{Mpc}^{-1}$. The reconstructed power spectrum can achieve a tighter constraint on $\nu$CDM cosmology.

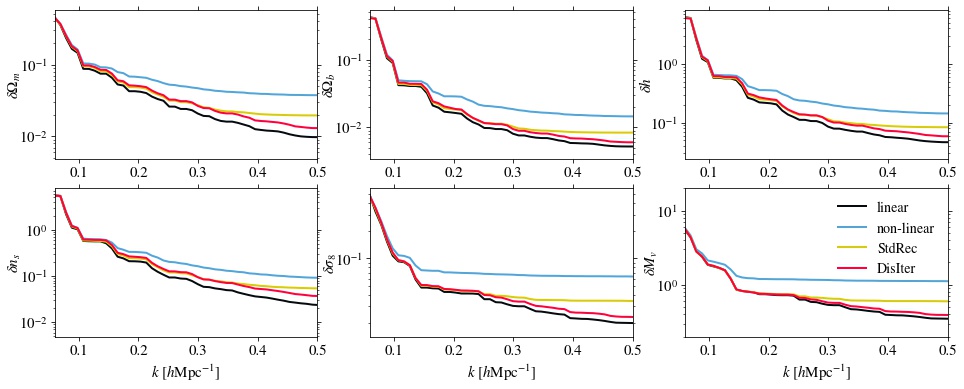
This figure shows the trend of the Fisher error when we include more and more small-scale information. On large scales, non-linear powewr and reconstructed power gives similar constraints on cosmological parameters. But when we go further into the non-linear regime, the reconstructed can extract more information from the density field than the non-linear power. This extra information comes from the high-order information of the original density field. Moreover, quite a part of the information comes from the BAO wiggle. The sharped BAO wiggle after reconstruction provides a better measurement of six parameters.

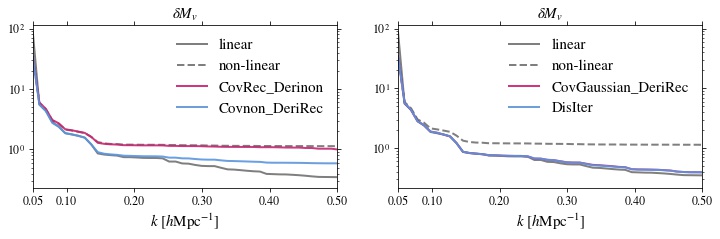
We also find that the retrieved information mainly comes from the reconstructed derivatives.